Harrell's little crib sheet on series
© Copyright 2000 by Evans M. Harrell II
Thou shalt know the following series:
-
The geometric series:
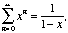 convergent for
|x| < 1
(variants)
convergent for
|x| < 1
(variants)
-
The arithmetic series:
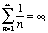 divergent even
though a0 tends to zero. The arithmetic series is
actually the borderline case for the p-series,
divergent even
though a0 tends to zero. The arithmetic series is
actually the borderline case for the p-series,  which converges if p > 1. However, there is no
simple formula for the sum of the general p-series.
which converges if p > 1. However, there is no
simple formula for the sum of the general p-series.
-
The
Taylor
series for
These converge for all x.
Fiddling with series
If series converge you can fiddle up other convergent series if you:
- add or subtract them
- multiply them (take care to collect terms correctly)
- plug them into each other
- perform calculus on them (for power series)
(See some
examples.)
Spotting elephants
In the Infinite Seriesian Jungle, there are only two
kinds of animals, elephants (divergent series) and bugs
(convergent series).
There are two basic ways to recognize elephants, i.e.,
to show that series diverge. Other tests for divergence are
really special cases of the comparison test.
- If the parts of the beast aren't small, it's an elephant.
(If an does not tend to 0, the series does not converge.)
- (comparison test)
If a beast in the jungle is bigger than an elephant,
it's another elephant!
Just as there are two kinds of elephants,
there are two ways a series can fail to converge. The
partial sums may tend to infinity, but another kind of divergence
("by oscillation") happens if they simply wander around finitely without ever committing themselves
(examples.)
Squashing series down
There are several ways to squash bugs in the jungle, i.e., to
show that a series converges.
Here we mention only a few of them.
Most tests for convergence use the
absolute values of an, because if the
absolute value series converges, then so does the
series where an can be positive or negative.
- (comparison test)
If a beast in the jungle is smaller (in absolute value)
than a bug,
it is another bug!
- (alternating series test)
If it has little parts and they wiggle back and forth, it's a
bug: If
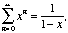 and the signs alternate (strictly, at least after the
first million), then the series converges.
and the signs alternate (strictly, at least after the
first million), then the series converges.
- (Taylor's formula with remainder) A series can be
proved to converge if you can recognize
it as a convergent Taylor series with some particular value of
x.
(examples)
Hunting for elephants or bugs
Some tests go both ways, but these are really special cases of the
comparison tests:
- (ratio test)
If
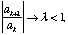 then the series converges. If
then the series converges. If
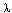 > 1, it diverges. If
> 1, it diverges. If
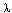 = 1, all bets are off.
= 1, all bets are off.
- (limit comparison test)
If bn > 0 and
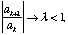 no matter how large L is, then the a series and the b series either
both converge or both diverge.
no matter how large L is, then the a series and the b series either
both converge or both diverge.
- (integral test)
If
a(x) is a positive function, then the series with an
converges or diverges together with the integral of a(x) from any
finite value to
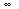 .
.
(examples)
Some tips
- If you are only asked about convergence, the first million or so
terms don't matter at all.
- A Taylor or power series becomes an ordinary series as soon as
you fix x. Usually, convergence of these series comes from either
Lagrange's formula or the ratio test.
- By its very nature, an error estimate is hardly ever exact. So,
simplify, simplify! Identify something bigger to replace something
ugly (like 1 in favor of cos(exp(x1/2)).
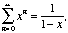 convergent for
|x| < 1
(variants)
convergent for
|x| < 1
(variants)
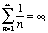 divergent even
though a0 tends to zero. The arithmetic series is
actually the borderline case for the p-series,
divergent even
though a0 tends to zero. The arithmetic series is
actually the borderline case for the p-series,  which converges if p > 1. However, there is no
simple formula for the sum of the general p-series.
which converges if p > 1. However, there is no
simple formula for the sum of the general p-series.
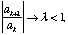 then the series converges. If
then the series converges. If
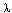 > 1, it diverges. If
> 1, it diverges. If
 .
.