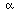 v|| =
|
v|| =
|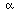 |
||v||
|
||v||
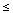 ||v|| + ||w||
||v|| + ||w||
DefinitionA Banach space is a vector space together with a norm, in the topology of which the vector space is complete.
That is, there is a mapping from B to R+, denoted ||v||, such that
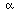 v|| =
|
v|| =
|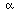 |
||v||
|
||v||
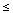 ||v|| + ||w||
||v|| + ||w||
Further, all Cauchy sequences with respect to the norm converge to limits in B.
It is normal to assume tacitly that a Banach space is infinite dimensional.
Some Banach spaces are Hilbert spaces. They are called Hilbert spaces when the norm is defined by an inner product, <v, w> by ||v||2 := <v, v>. A norm can be defined in terms of an inner product iff it satisfies the parallelogram identity.