Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 8 September 1996
Newton articulated some principles of heat flow through solids, but it was Fourier who created the correct systematic theory. Inside a solid there is no convective transfer of heat energy and little radiative transfer, so temperature changes only by conduction, as the energy we now recognize as molecular kinetic energy flows from hotter regions to cooler regions. The first basic principle of heat is:
1. the heat energy contained in a material is proportional to the temperature, the density of the material, and a physical characteristic of the material called the specific heat capacity. In mathematical terms,
(8.a1)
For the other principles of heat transfer, let us do some experiments with the
following materials: a hot stove, some iron rods of different,
relatively short lengths and various widths, and various ceramic rods of
different lengths and widths. Since these will be thought experiments only, it
will be safe to use a finger as the probe. Putting your finger right on the
stove will convince you that the energy transfer is proportional to the
difference in temperature between your finger and the stove. Using, if
necessary, a different, undamaged finger, you will also find that the rate of
heat transfer is inversely proportional to the length of an iron rod
intervening between your finger to the stove (fixing the cross-sectional
area). In other words, the rate of heat flow from one region to another is
proportional to the temperature gradient between the two regions. You will
probably also agree that the rate of heat flow will be proportional to the area
of the contact; for example, a short pin with one end on a hot stove and the
other touching your hand is preferable to putting the palm of your hand on a
frying pan. Finally, a ceramic material on the stove being usually more
pleasant to the touch than hot iron, we see that the rate of heat transfer
depends on the material, as measured with a physical constant known as the
heat conductivity
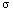 . The second basic principle is thus:
. The second basic principle is thus:
2. The heat transfer through the boundary of a region is proportional to the
heat conductivity,
to the gradient of the temperature across the region, and to
the area of contact, so
then
If we differentiate eq. (8.a1) with respect to time and apply Gauss's divergence theorem to (8.a2), we find that dQ/dt can be expressed in two ways as an integral:
Since the region
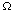 can be an arbitrary piece of the material under
study, the integrands must be equal at almost
every point. If the material under study is a slab of a homogeneous
substance, then
can be an arbitrary piece of the material under
study, the integrands must be equal at almost
every point. If the material under study is a slab of a homogeneous
substance, then
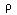 ,
,
 s, and
s, and
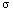 are independent of the
position x, and we obtain the heat equation
are independent of the
position x, and we obtain the heat equation
,
where k =
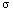 /
/
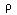
 s. Ordinary substances have values of k
ranging from about 5 to 9000 cm2/gm (see
table).
s. Ordinary substances have values of k
ranging from about 5 to 9000 cm2/gm (see
table).
The one-dimensional heat equation
ut = k uxx
would apply, for instance, to the case of a long, thin metal rod wrapped with insulation, since the temperature of any cross-section will be constant, due to the rapid equilibration to be expected over short distances.
Return to Chapter VIII
Return to Table of Contents
Return to Evans Harrell's home page