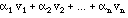
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
version of 5 August 1996, text with Maple. A Mathematica version is also available.
If you wish to print a nicely formatted version of this chapter, you may download the rtf file, which will be interpreted and opened by Microsoft Word.
(Some remarks for the instructor).
This course is concerned with some of the most important methods of applied mathematics, without which many technological developments of the nineteenth and twentieth centuries would have been impossible. When you have finished this course you will be able to solve most of the partial differential equations and integral equations that you are likely to encounter in engineering, and, just as importantly, you will understand what to expect from the solutions, which might emerge in a mysterious fashion from a computer at your workplace. You will also learn techniques that are useful in other contexts - Fourier series, special functions, and iteration.
The leitmotifs are linearity and orthogonality. By this stage inyour education, you are familiar with vectors. You have added them by thehead-to-tail construction, or by adding their components. You also know how to take their scalar (dot) product, producing a number equal to the product of the two lengths and the cosine of the angle between them:
v.w = |v| |w| cos(angle(v,w))
One of the most powerful and astonishing ideas in modern mathematics is that in many regards functions can be treated just like vectors. There is a very close analogy between sets of functions and spaces of vectors, which will guide us to striking solutions to several of the most important differential equations you will use in science and engineering, especially the wave equation, the heat equation, and the potential equation.
Mathematicians have a way of making analogies without the mushiness that so often afflicts analogies in so many other contexts. It is called abstraction. While abstraction may sometimes seem like theory divorced from reality, when used properly it is a wonderful, and very practical, tool for solving problems.
This is why we will begin by making vectors abstract. Let us recall some facts about everyday vectors. If I have a bag full of vectors, I can add scale them and add them together. We call the result a linear combination:
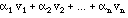
I'll normally use Greek letters for scalars (= ordinary real or complex numbers). It doesn't matter how many are in the combination, but unless I explicitly state otherwise, I will assume that it is only a finite sum, a finite linear combination. Of course, we can make linear combinations of functions, too:
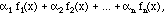
and that is another function. In this way, the set of all functions is a vector space.
Definition I.1. More formally, a vector space over the complex numbers is a set of entities, abstractly called vectors, for which
1. Any finite linear combination of vectors is a member of the same set
2. The usual commutative rule holds for addition: v + w = w + v,
3. Just for consistency, the usual commutative, associative, and distributive laws hold for vector addition and multiplication by scalars. In other words
 ,
,
 ,
,
 .
.
Also, 1 v = v.
In practice the rules in 3 are obvious and not very interesting. From these rules, you can show some other properties, such as:
There is a special element, which will be called the zero vector, equal to the scalar 0 times any vector whatsoever. It has the property that for any vector v, 0 + v = v.
For any vector v, there is a negative vector, called -v, such that v + (-v) = 0 (the zero vector).
Certain pretty reasonable conventions will be made, such as writing v - w instead of v + (- w). Great - all the usual stuff works, right? Well, not quite. We don't assume abstractly that we can multiply vectors by one another. Things like the dot product and the cross product work for some vector spaces but not for others. The other deep issue lurking in the shadows is infinite linear combinations, i.e., infinite series. Fourier liked them, and we'll see lots of them later. But if the vectors are functions, perhaps the infinite series converges for some x and not for others. For instance,
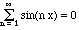
when x is a multiple of pi, but it is certainly an improper sum when x = pi/2, and it is not immediately clear what happens for other values of x. What does the series mean then?
1. The usual two-dimensional or three-dimensional vectors, which can be thought of as column vectors such as
[2] [3]
or as row vectors (2,3). In Maple's notation, vectors are represented as lists, that is, a string of items within brackets: [2,3]. The set of all such vectors will be denoted C2 or C3 (assuming complex entries are allowed - otherwise R2 or respectively R3). Maple manipulates them in a straightforward way. First we need to let Maple know we are doing linear algebra (Note the colon).
with(linalg):evalm([2,3]+[4+I,2]); [6+I, 5]
(I is the square root of -1 in Maple, and evalm stands for "evaluate matrix," since Maple regards a vector as a matrix with only one row or column.) For the dot product,
dotprod([2,3],[1,2]); 8
2. The set of complex numbers. Here there is no difference between a vector and a scalar, and you can check all the properties pretty easily. We call this a one-dimensional vector space.
3. The set Cn of n numbers, manipulated just like 2- or 3- vectors, except that the number of components is some other fixed number, n. For instance,with C4, we might have elements such as [1,2,3,4] and [1,0,-1,-2]
evalm([1,2,3,4]+[1,0,-1,-2]); [ 2, 2, 2, 2 ]dotprod([1,2,3,4],[1,0,-1,-2]); -10evalb("=1*1+2*0+3*(-1)+4*(-2)); true
(The ditto mark " refers to the result of the previous calculation in Maple, and evalb, short for "evaluate Boolean," treats the input as a logical variable. This is a convenient way to check two calculations which do not look identical.
4. The set of continuous functions of a variable x, 0 < x < 1. The rather stupid function f0(x) = 0 for all x plays the role of the zero element.
5. Instead of listing n numbers, let us multiply them by n different functions, to define another vector space of functions. For example, for some fixed n, consider
a1 sin(x) + a2 sin(2x) + ... + an sin(nx),
where the numbers ak can take on any value. Notice that this vector space is a part of the previous one, in other words, a subspace .
6. The set of, say, 2 by 3 matrices. Addition means addition component-wise:
[1 0 i ] [2 -i 0 ] [3 -i i]
[-1 pi 2+i] + [-1 -pi 2-i] = [-2 0 4]
and multiplication by scalars affects all components:
[1 0 i ] [5 0 5i ]
5 [-1 pi 2+i] = [-5 5 pi 10+5i]
In Maple a matrix is a list of lists - after all it consists of a string of row vectors:
m1:=[[1,0,I],[-1,Pi,2+I]]; m1:=[[1,0,I],[-1,\pi,2+I]];m2:=[[2,-I,0],[-1,-Pi,2-I]]; m1:=[[2,-I,0],[-1, -\pi,2-I]];evalm(m1+m2); m2 := [[2, - I, 0], [-1, - Pi, 2 - I]]evalm(5*m1); [ 5 0 5 I ] [ ] [ -5 5 Pi 10 + 5 I ]
7. The set of 3-component vectors (x,y,z) such that x - 2y + z = 0. This is a plane through the origin.
Definitions I.3. A set of vectors {v1, ..., vn} is linearly independent if it is impossible to write any of the vectors in the set as a linear combination of the rest. Linearly dependent is the opposite notion. The dimension of a vector space V is the largest number n of linearly independent vectors {v1, ..., vn} which are contained in V. The span of a set {v1, ..., vn} is the vector space V obtained by considering all possible linear combinations from the set. We also say that {v1, ..., vn} spans V. A set {v1, ..., vn} is a basis for a finite-dimensional vector space V if {v1, ..., vn} is linearly independent and spans V.
Notice that the only way that two vectors can be linearly dependent is for them to be proportional (parallel) or for one of them to be 0. If the set has the same number of vectors as each vector has components, which frequently is the case, then there is a calculation to test for linear dependence. Array the vectors in a square matrix and calculate its determinant. If the determinant is 0, they are dependent, and otherwise they are independent. For example, consider the vectors {(1,2,3), (4,5,6),(7,8,9)}, which are not obviously linearly dependent. A calculation with Mathematica shows:
In:= Det[{{1,2,3},{4,5,6},{7,8,9}}]
Out= 0
Indeed, we can solve for one of these vectors as a linear combination of the others:
In:= Solve[{7,8,9} == alpha {1,2,3} + beta {4,5,6}, {alpha, beta}]
Out= {{alpha -> -1, beta -> 2}}
Many of our vector spaces will be infinite-dimensional. For example, {sin(n x)} for n = 1, 2, ..., is an infinite, linearly independent set of continuous functions - there is no way to write sin(400 x), for example, as a linear combination of sine functions with lower frequencies, so you can see that each time we introduce a sine function of a higher frequency into the list, it is independent of the sines that were already there. An infinite linearly independent set is a basis for V is every element of V is a limit of finite linear combinations of the set - but we shall have to say more later about such limits. A vector space has lots of different bases, but all bases contain the same number of items.
For practical purposes, the dimension of a set is the number of degrees of freedom, i.e., the number of parameters it takes to describe the set. For example, Cn has dimension n, and the set of 2 by 3 matrices has six elements, so its dimension is 6.
Model problem I.4. Show that the plane x + y + z = 0 is a two-dimensional vector space.
The verification of the vector space properties will be left to the reader. Here is how to show that the dimension is 2:
Solution. The solution can't be 3, since there are vectors in R3 which are not in the plane, such as (1,1,1). On the other hand, here are two independent vectors in the plane: (1,-1,0) and (1,1,-2).
solve({x=alpha*1+beta*1,y=alpha*(-1)+beta*(1)}, {alpha, beta}); {alpha = - 1/2 y + 1/2 x, beta = 1/2 x + 1/2 y}
Hence the two vectors we found in the solution are a basis for the plane. Any two independent vectors in the plane form a basis.
Definition I.5. A linear transformation is a function on vectors, with the property that it doesn't matter whether linear combinations are made before or after the transformation. Formally,
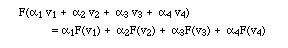
Linear transformations are also called linear operators, or just operators for short. You know plenty of examples:
Examples I.6.
1. Matrices. If M is a matrix and v, w etc. are column vectors, then
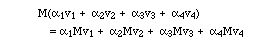
Think of rotation and reflection matrices here. If you put a bunch of vectors head-to-tail and rotate the assemblage, or look at it in a mirror, you get the same effect as if you first rotate or reflect the vectors, and then put them head-to-tail. It may be less geometrically obvious when the matrix distorts vectors in a trickier way, or there are more than three dimensions, but it is still true.
2. Derivatives and integrals. As we know,
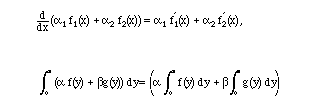
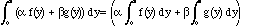
As Maple puts it:
evalb(diff(alpha*f(x)+beta*g(x),x)=alpha*diff(f(x),x)+beta*diff(g(x),x)); True
3. This may seem silly at first, but the identity operator Id, which just leaves functions alone is a linear transformation:
,
since both sides are just round-about ways of writing alpha1 f1 + alpha2f2. The identity operator is a useful bit of notation for much the same reason as the identity matrix,
[1 0 0] Id = [0 1 0] [0 0 1]
the effect of which on any vector is to leave it unchanged.
A linear transformation is a function defined on vectors, and the output is always a vector, but the output need not be the same kind of vector as the input. You should be familiar with this from matrices, since a 2 by 3 matrix acts on 3-vectors and produces 2-vectors. Similarly, the operator D acts on a vector space of functions assumed to be differentiable and produces functions which are not necessarily differentiable.
Example I.7. More exotic possibilities are possible, such as the operator which acts on 2 by 2 matrices by the rule:
![F[{{m_11,m_12},{m_21,m_22}}] = m_11 sin(x) - 3 m_22 sin(2x)](pix/Ii.gif)
The whole theory we are going to develop begins with the analogy between Example I.3.1 and Example I.3.2. We can think of the linear operator of differentiation by x as a kind of abstract matrix, denoted D (as inMathematica, where f'[x] can be written D[f[x],x]; in Maple, this correspondsto diff) . If we also think of the functions f and g as entities unto themselves, without focusing on the variable x, then the expression in thefirst part of Example I.3.2 looks a whole lot like Example I.3.1:
,
The custom with linear transformations, as with matrices, is to do without the parentheses when the input variable is clear. It is tempting to manipulate linear operators in many additional ways as if they were matrices, for instance to multiply them together. This often works. For instance D2 = D D can be thought of as the second derivative operator, and expressions such as D2 + D + 2 Id make sense. In passing, notice that if S is the integration operator of the second part of Example 2, then D S f = f, so D is the inverse to S in the sense that D S = Id. (But is S D = Id?)
Linear ODE's. In your course on ordinary differential equations, you studied linear differential equations, a good example of which would be
D2y + Dy + 2y = 0
More specifically, this is an example of a "linear, homogeneous differential equation of second order, with constant coefficients". We can picture this equation as one for the null space of a differential operator A:
A y := (D2 + D + 2 Id) y = 0. (1.1)
(Maple renders this as
A:=u->diff(diff(u,x),x)+diff(u,x)+2*u; / 2 \ | d | / d \ A := u -> |----- u| + |---- u| + 2 u | 2 | \ dx / \ dx /
By definition, the null space N(A) is the set of all vectors solving this equation; some texts refer to it as the kernel of A. There is no difference. You may remember that the null space of a matrix is always a linear subspace, and the same is true for the null space of any linear operator. E. g., the plane of Example 1.2.6 is the null