(c) Copyright 1994,1995 by Evans M. Harrell, II. All rights reserved
In[2]:=
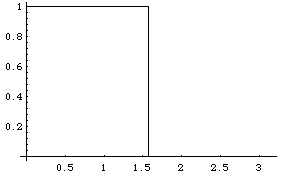
f[x_,L_] := 1 /; 0 <= x <= L/2
f[x_,L_] := 0 /; L/2 < x <= L
In[3]:=
Plot[f[x,Pi], {x, 0, Pi}]
Out[3]=

-Graphics-
In[4]:=
a[0] := (1/L) Integrate[f[x,L], {x,0,L}]
In[5]:=
a[0]
Out[5]=
1 - 2
When calculating the Fourier coefficients with Mathematica, it is often useful to inform Mathematica of some simplifications of the trig functions, with a command such as
In:= TrigId = {Cos[Pi n_] -> (-1)^n, Sin[Pi n_] -> 0}
Out:= {Cos[Pi*(n_)] -> (-1)^n, Sin[Pi*(n_)] -> 0}
This tells the software to replace Cos[Pi n] with (-1)^n wherever it is
encountered. (If n were not an integer, this would not be true.)
In[6]:=
TrigId = {Cos[Pi n_] -> (-1)^n, Sin[Pi n_] -> 0}
Out[6]=
n
{Cos[Pi (n_)] -> (-1) , Sin[Pi (n_)] -> 0}
In[7]:=
a[m_,L_] := (2/L) Integrate[Cos[2 m Pi x/L], {x,0,L/2}]
In[8]:=
a[m,Pi]
Out[8]=
Sin[m Pi]
---------
m Pi
In[9]:=
% /. TrigId
Out[9]=
0
These coefficients are all zero. Why?
In[10]:=
b[n_,L_] := (2/L) Integrate[Sin[2 n Pi x/L], {x,0,L/2}]
In[11]:=
b[n,Pi] /. TrigId
Out[11]=
n
1 (-1)
2 (--- - -----)
2 n 2 n
---------------
Pi
In[12]:=
Simplify[%]
Out[12]=
n
1 - (-1)
---------
n Pi
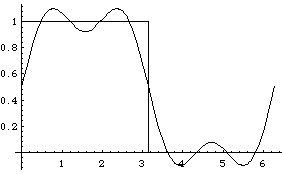
If n is even, b[2 k] = 0. Thus only odd terms survive, in which case
b[2 k + 1] = 2/(Pi (2 k + 1)). We can write the full series:
In[13]:=
Clear[FullSeries]
In[14]:=
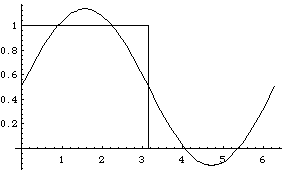
FullSeries[x_,N_,L_] := 1/2 + \
Sum[2 Sin[2 Pi n x/L]/ (Pi n),{n,1,N,2}]
In[15]:=
Plot[{FullSeries[x,1, 2 Pi], f[x,2 Pi]}, {x,0,2 Pi}]
Out[15]=
-Graphics-
In[16]:=
Plot[{FullSeries[x,3, 2 Pi], f[x,2 Pi]}, {x,0,2 Pi}]
Out[16]=
-Graphics-
In[17]:=
Plot[{FullSeries[x,7, 2 Pi], f[x,2 Pi]}, {x,0,2 Pi}]
Out[17]=

-Graphics-
We can now investigate some questions about the excitation of mechanical
resonances.
Suppose that experiments by K. Battle at the Wiener Staa