(c) Copyright 1996 by Evans M. Harrell, II. All rights reserved
In[1]:=
Integrate[Sin[Pi(x-t)], {t,0,x}]
Out[1]=
1 Cos[Pi x] -- - --------- Pi Pi
This is maximized by 2/¹, which is less than 1:
In[2]:=
N[2/Pi]
Out[2]=
0.63662
We are thus guaranteed that the integral equation has a continuous solution,
and that we can calculate it by iteration.
To see if the kernel is small in the sense appropriate for a square-integrable
solution y(x), we calculate:
In[3]:=
Integrate[Sin[Pi(x-t)]^2, {t,0,x}]
Out[3]=
-(-2 Pi x + Sin[2 Pi x])
------------------------
4 Pi
In[4]:=
Integrate[%, {x,0,1}]
Out[4]=
2
-1 1 + 2 Pi
----- + ---------
2 2
8 Pi 8 Pi
In[5]:=
N[%]
Out[5]=
0.25
This is also less than 1, so we are guaranteed that iteration will lead us to
the solution in the r.m.s. sense. Normally this is a weaker statement than the
previous one, so we are not surprised.
Now let's calculate the solution
In[6]:=
Clear[K]
In[7]:=
K[f_] := Integrate[Sin[Pi(x-t)] (f /. x -> t), {t,0,x}]
The obscure command embedded in this, (f /. x -> t), has the effect of changing the variable in the function f from x to t, which we need to do to integrate properly.
In[8]:=
y1[x_] = K[x]
Out[8]=
x Sin[Pi x]
-- - ---------
Pi 2
Pi
In[9]:=
y2[x_] = K[y1[x]]
Out[9]=
4 Pi x + 2 Pi x Cos[Pi x] - Sin[Pi x] 5 Sin[Pi x]
------------------------------------- - -----------
3 3
4 Pi 4 Pi
In[10]:=
y3[x_] = K[y2[x]]
Out[10]=
-23 Sin[Pi x]
------------- + (16 Pi x + 14 Pi x Cos[Pi x] -
4
16 Pi
2 2 4
7 Sin[Pi x] + 2 Pi x Sin[Pi x]) / (16 Pi )
In[11]:=
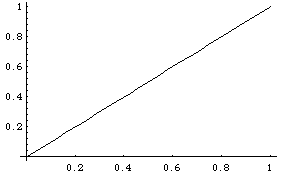
{Plot[x, {x,0,1}], Plot[y1[x]+x, {x,0,1}], \
Plot[y2[x]+y1[x]+x, {x,0,1}], \
Plot[y3[x]+y2[x]+y1[x]+x, {x,0,1}]}

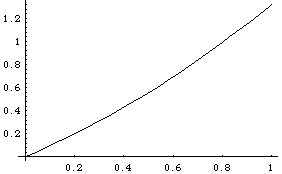
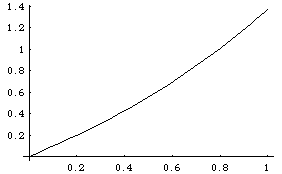
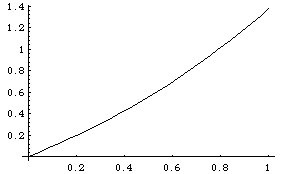
Out[12]=
{-Graphics-, -Graphics-, -Graphics-, -Graphics-}
These last two plots look somewhat similar, which is an indication that we are
getting close to the exact solution. How far away are we? Well, if you stop the
series at third order,
f + Kf + K2 f + K3 f,
then the error is K4 f + K5 f +...
We know that the calculations we must check for convergence are actually bounds
of the form ||K g|| <= c || g||,
where for the infinity norm (for continuous functions), c = 2/ \pi, and for the
r.m.s. norm (for square-integrable functions) c = 1/2. (The calculation we did
gave 1/4, but that is actually c2).
The right scale for this problem is ||x||infinity = 1 or, respectively, ||x||2
= 1/Sqrt[3]
In[13]:=
N[1/Sqrt[3]]
Out[13]=
0.57735
The norm of Kn f is at most cn times the norm of f (either norm), so the size
of the error is
c4 + c5 + ... = c4 (1 + c + c2 + ...) = c4/(1-c).
Conclusion: The maximum possible error
|x+y1+y2+y3 - yexact(x)|
is at most
In[14]:=
N[(2/Pi)^4 /(1-2/Pi)]
Out[14]=
0.452022
The maximum possible error in the rms sense is
In[15]:=
(1/2)^4 / (1-1/2)
Out[15]=
1 - 8
Which is fairly small. If we want more accuracy, we need more terms. With 8 terms,
In[16]:=
N[(2/Pi)^8 /(1-2/Pi)]
Out[16]=
0.0742471
In[17]:=
N[(1/2)^7]
Out[17]=
0.0078125
So we would be within 5% uniformly and about 1% in the rms sense. Actually, we are probably doing much better, for already at third order,
In[18]:=
Plot[y3[x], {x,0,1/2}]
Plot[y3[x], {x,1/2,1}]
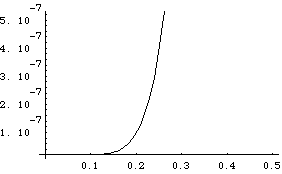
Out[19]=
-Graphics-
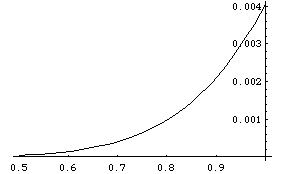
Out[20]=
-Graphics-
In[21]:=
y4[x_] = K[y3[x]]
y5[x_] = K[y4[x]]
y6[x_] = K[y5[x]]
y7[x_] = K[y6[x]]
y8[x_] = K[y7[x]]
Out[21]=
-51 Sin[Pi x]
------------- + (96 Pi x + 114 Pi x Cos[Pi x] -
5
32 Pi
3 3 2 2
2 Pi x Cos[Pi x] - 57 Sin[Pi x] + 24 Pi x Sin[Pi x]
5
) / (96 Pi )
Out[22]=
-443 Sin[Pi x]
-------------- + (768 Pi x + 1122 Pi x Cos[Pi x] -
6
256 Pi
3 3
36 Pi x Cos[Pi x] - 561 Sin[Pi x] +
2 2 4 4 6
282 Pi x Sin[Pi x] - 2 Pi x Sin[Pi x]) / (768 Pi )
Out[23]=
-949 Sin[Pi x]
-------------- + (7680 Pi x + 13110 Pi x Cos[Pi x] -
7
512 Pi
3 3 5 5
570 Pi x Cos[Pi x] + 2 Pi x Cos[Pi x] -
2 2
6555 Sin[Pi x] + 3660 Pi x Sin[Pi x] -
4 4 7
50 Pi x Sin[Pi x]) / (7680 Pi )
Out[24]=
-4027 Sin[Pi x]
--------------- + (92160 Pi x + 178110 Pi x Cos[Pi x] -
8
2048 Pi
3 3 5 5
9360 Pi x Cos[Pi x] + 66 Pi x Cos[Pi x] -
2 2
89055 Sin[Pi x] + 53370 Pi x Sin[Pi x] -
4 4 6 6
1020 Pi x Sin[Pi x] + 2 Pi x Sin[Pi x]) /
8
(92160 Pi )
Out[25]=
-8483 Sin[Pi x]
--------------- + (1290240 Pi x + 2763810 Pi x Cos[Pi x] -
9
4096 Pi
3 3 5 5
165690 Pi x Cos[Pi x] + 1680 Pi x Cos[Pi x] -
7 7
2 Pi x Cos[Pi x] - 1381905 Sin[Pi x] +
2 2 4 4
871920 Pi x Sin[Pi x] - 20580 Pi x Sin[Pi x] +
6 6 9
84 Pi x Sin[Pi x]) / (1290240 Pi )
What beautiful functions! How would you like to calculate them by hand?
You can hardly see the difference between the really accurate solution and the third order solution:
In[26]:=
Plot[{x+y1[x]+y2[x]+y3[x]+y4[x]+y5[x]+y6[x] \
+ y7[x]+y8[x], \
x+y1[x]+y2[x]+y3[x]}, {x,0,1}]
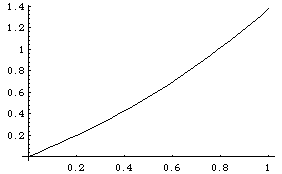
Out[27]=
-Graphics-
In[28]:=
Plot[{x+y1[x]+y2[x]+y3[x]+y4[x]+y5[x]+y6[x] \
+ y7[x]+y8[x], \
x+y1[x]+y2[x]+y3[x]}, {x,.99,1}]
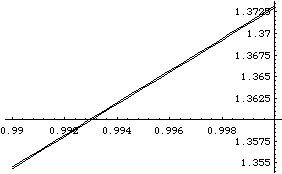
Out[29]=
-Graphics-
Up to chapter 5Return to Table of Contents
Return to Evans Harrell's home page