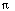 2 t) cos(n
2 t) cos(n
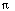 x)/(n2
x)/(n2 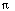 2).
2).
Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
1.
a) Solve the following problem:
PDE ut = 4 uxx, for 0 < t, 0 < x < 1
BC ux(t,0) = 0, ux(t,1) = 0, for 0 < t
IC u(0,x) = 2 x - x2, for 0 < x < 1
ANSWER:
u(t,x) = 2/3 - 4 Sum exp(-4 n2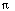 2 t) cos(n
2 t) cos(n
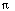 x)/(n2
x)/(n2 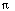 2).
2).
The way to get this solution is to recall that the separated solutions with these BC are either constants or of the form constant exp(-4 n2 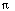 2 t) cos(n
2 t) cos(n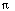 x)/(n2. The general solution is a sum of these solutions, with coefficients we could call an. When we put t = 0, we get a Fourier cosine series, and the coefficients are the Fourier cosine coefficients for 2 x - x2. Then use the standard formula for these coefficients.
x)/(n2. The general solution is a sum of these solutions, with coefficients we could call an. When we put t = 0, we get a Fourier cosine series, and the coefficients are the Fourier cosine coefficients for 2 x - x2. Then use the standard formula for these coefficients.
b) Find the maximum value of u(t,x) for 0 <= t <= 1, 0 <= x <= 1:
We know by the maximum principle that the maximum value occurs either at t=0, t = 1, x = 0, or x = 1, so only these values need to be considered. Physical reasoning can be used, if you wish, to eliminate all possibilities for t > 0 (the rod is insulated and has no sources, so heat cannot appear at the ends while the temperature relaxes to equilibrium). Considering t=0, we find:
ANSWER:
The maximum temperature occurs at x = 1, t = 0
The maximum temperature is umax = 1
There is a complete, orthonormal set of functions denoted
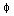 n(x), for
-infinity < x < infinity, which are eigenfunctions for the
ordinary differential equation
n(x), for
-infinity < x < infinity, which are eigenfunctions for the
ordinary differential equation
- 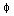 n'' + x2
n'' + x2
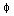 n = (2n+1)
n = (2n+1) 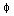 n, n = 0, 1, 2,
....
n, n = 0, 1, 2,
....
You may use the notation 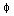 n in the answer to this problem.
n in the answer to this problem.
Consider the following PDE:
PDE utt = grad2 u - x2 u, for 0 < t, 0 < x < 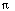 1, 0 < y <
1, 0 < y < 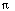
BC u(t,x,0) = u(t,x, 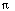 ) = 0, for 0 < t
) = 0, for 0 < t
Find the normal mode with the lowest frequency of vibration (include the time dependence):
ANSWER:
This is a straightforward separation of variables, albeit with a new function. The function Y satisfies the usual eigenvalue equation with 0 Dirichlet BC, so the spatial part of the separated solutions are of the form
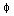 n sin(m y), n = 0, 1, ...; m = 1, 2, .... If the full solution is of the form Tnm(t)
n sin(m y), n = 0, 1, ...; m = 1, 2, .... If the full solution is of the form Tnm(t)
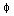 n(x) sin(m y), then substituting into the PDE shows that
n(x) sin(m y), then substituting into the PDE shows that
Tnm''(t) = 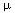 nm Tnm(t),
nm Tnm(t),
where 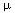 nm = (2 n + 1) + m2. The solutions are sines and cosines of
nm = (2 n + 1) + m2. The solutions are sines and cosines of 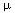 nm1/2. The lowest frequency occurs when m = 0, n = 1:
nm1/2. The lowest frequency occurs when m = 0, n = 1:
u(t,x,y) = (A01 cos(21/2 t) + B01 sin(21/2 t) ) 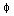 0(x) sin(y),
0(x) sin(y),
or, if you prefer,
u(t,x,y) = (A01 cos(21/2 t) + B01 sin(21/2 t) ) exp(-x2/2) sin(y).
Find the general solution:
ANSWER:
u(t,x,y) = Sum of (Anm cos((2n+1+m2)1/2 t) + Bnm sin((2n+1+m2)1/2 t) )
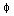 n(x) sin(m y), for n = 0, 1, ...; m = 1, 2, ....
n(x) sin(m y), for n = 0, 1, ...; m = 1, 2, ....
0 < r < 20 cm,
0 <  <
< 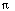 /3 radians
/3 radians
0 < z < 1 cm.
It has come to thermal equilibrium while sitting on a student's computer monitor, so that the temperature on its surface is
u(r,  , 0) = 30
, 0) = 30
u(r,  , 1) = 20
, 1) = 20
u(r,0,z) = u(r, 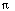 /3,z) = 30 - 10 z
/3,z) = 30 - 10 z
u(20,  ,z) = 30 - 10 z - 5
,z) = 30 - 10 z - 5
This is a low quality pizza consisting of a homogeneous material (independent of position)
a) The partial differential equation for a homogeneous material at thermal equilibrium is Laplace's equation,
grad2 u = 0
b) Answer the following questions.
Are there useful simplifications involving the boundary conditions? If so, what are they?
Be specific and put the answer here: Most of the boundary conditions can be made homogeneous by redefining the unknown as
v(t,x) = u - (30 - 10 z).
The only BC which remains nonhomogeneous is the one at r = 20.
Are there useful separated solutions? If so, write the specific ordinary differential equations that the separated solutions satisfy below. Include boundary conditions.
write v(r, , z) = R(r) Q(
, z) = R(r) Q( ) Z(z). Then:
) Z(z). Then:
- Q'' = 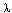 Q,
Q,
 (0) =
(0) =  (
(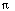 /3) = 0
/3) = 0
- Z'' = 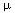 Z,
Z,
Z(0) = Z(1) = 0
R'' + (1/r) R' = (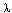 /r2 +
/r2 + 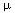 ) R,
) R,
R(0) bounded
(We don't do anything about the nonhomogeneous boundary before putting the separated solutions together.)
c) Solve the differential equations with the given boundary conditions.
The equation for R is our old friend Bessel's equation, but the eigenvalues 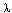 are now determined by the conditions on Q, which lead to eigenfunctions of the
form sin(3 m
are now determined by the conditions on Q, which lead to eigenfunctions of the
form sin(3 m  ) and
eigenvalues
) and
eigenvalues 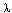 m = 9 m2.
m = 9 m2.
Back to Chapter X
Return to Table of Contents
Return to Evans Harrell's home page