Examples of convergence

Linear Methods of Applied Mathematics

Evans M. Harrell II and James V. Herod*

*(c) Copyright 1994,1997,2000 by Evans M. Harrell II and James V. Herod. All rights reserved.

version of 23 February 2000

Here are two examples illustrating different ways in which a sequence of functions can converge. To illustrate these ideas, two examples follow. In the first, there is a sequence {fp} and a function g in the space with

limn fn = g. In the second, there is no such g.

Example C.1: Let E be the vector space of continuous functions on [0,1] with the usual inner product. Let

fn(x) = BLC{(A(1/n if 0 <= x <= 1/n, x if 1/n <= x <= 1))

and let g(x) = x on [0,1]. Then limn I|fn - g||2

= lim<sub>n</sub> I(0,1, ) [ fn(x)-g(x) ]<sup>2</sup> dx = lim n I(0,1/n, ) (1/n - x)<sup>2</sup> dx = 0.

As in Chapter II, we say that fn converges in the root-mean-square, or L2, sense.

Example C.2. This space E of continuous functions on [0,1] with the "usual" inner product is not complete. To establish this, we provide a sequence fp for which there is no continuous function g such that limn fn = g.

fn(x) = BLC{(A(0, n(x- 1/2) + 1/2, 1))A(if 0 <= x <= (n-1)/2n, if (n-1)/2n <= x <= (n+1)/2n,if (n+1)/2n <= x <= 1) Sketch the graphs of f1, f2, and f3 to see that the limit of this sequence of functions is not continuous.

In chapter III we introduced the notion of uniform convergence. Recall:

Definition III.7. A sequence of functions {fk(x)} converges uniformly on the set 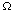Omega to a function g provided that

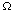|fk(x) - g(x)| < ck,             (*) where ck is a sequence of constants (independent of x in Omega) tending to 0.

Some terminology you may encounter for condition (*) is that the sequence fk(x) is Cauchy in the uniform sense. This condition guarantees that it converges uniformly to a limit, and that the limit is continuous:

Theorem. Suppose that x ranges over a closed, bounded set 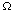Omega. If m > n implies that

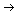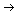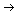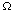|fn(x) - fm(x) | < cn, where the constants (independent of x) cn -> 0 as n -> 0, then there is a continuous function g(x) such that fk(x) -> g(x) uniformly on Omega.
Link to
  • chapter II
  • chapter III
  • chapter XV
  • Table of Contents
  • Evans Harrell's home page
  • Jim Herod's home page