Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod*
Recall that L2[0,1] is an inner product space when we provide it with the "usual" inner product. You should also recall there are many choices that can be made for an inner product for the functions on [0,1]. One might have a weighted inner product such as we had in Rn and as was described in an appendix to Chapter II. That is, if w(x) is a continuous, non-negative function, we might have
The choices for w(x) are usually suggested by the context in which the space arises.
Some inner product spaces are called Hilbert spaces.
Definition XV.1. A Hilbert space is a vector space on which there is an inner product and on which there is one more bit of structure: It is a complete inner product space, in the sense that if fp is an infinite sequence of vectors in the space which is Cauchy convergent - meaning that
limn,m < fn-fm , fn-fm > = limn,m | fn-fm |2 = 0
- then there is a vector g, also in the space, such that limn fn = g.
Take this opportunity to review the subject of inner-product spaces in chapter II or follow this link for two examples illustrating the notion of convergence in the Riesz representation theorems cast light on the nature of continuous linear transformations on function space. You may recall that in Rn, if L is a linear function from Rn to R then there is a vector v in Rn such that L(x) = < x, v > for each x in Rn. (More description of the analogue of Riesz representation for Rn.)
In general, where the vector space is not Rn, more is required.
Theorem XV.2. (The Riesz representation theorem for Hilbert space.) If {E, < , >} is a Hilbert space, then these are equivalent:
(a) L is a continuous, linear function from E to R (or the complex numbers C), and
(b) there is a unique member v of E such that L(x) = < x, v > for each x in E.
It is not hard to show that (b) implies (a). To show that (a) implies (b) is more interesting. The argument uses the fact that E is complete and can be found in any introduction to Hilbert space or functional analysis, or this link.
Example XV.3. Since the space of continuous functions on [0,1], denoted C[O,1], with the usual inner product is not a Hilbert space, one should expect that there might be a linear function L from C[0,1] to R for which there is no v in C[0,1] such that
for each f in C[0,1]. In fact, here is such an L:
Let
The candidate for v is v(x) =1 on [3/4, 1] and 0 on [0, 3/4). But this v is not continuous! It is only piecewise continuous.
Definition XV.4. The Heaviside function H is defined as follows:
(15.1)
Note that
Thus, the Heaviside function provides an element v for which the linear function
has a Riesz representation. As noted, v is not in C[0,1].
It is not always possible to have a piecewise continuous v which will rectify the situation. Consider the following linear function: L(f) = f(1/2). It is not so hard to see that there is no piecewise continuous function v on [0,1] having the property that for every continuous f,
Definition XV.5. The symbol
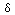 is used to denote the "generalized" function
which has the property that
is used to denote the "generalized" function
which has the property that
(15.2)
for some suitably large class of functions f, when 0 < a < 1. It is no surprise that some effort has been made to develop a theory of generalized functions in which the delta function can be found. Generalized functions are also called "distributions". While the delta function is not a well-defined function of the familiar type, it can be manipulated like a function in most cases, provided that in the end it will be integrated, and that the other quantities in the integral with it will be continuous.
A suggestive analogy is that of complex numbers. Like complex numbers, generalized functions are idealizations which do not describe real, physical things, but they have been found tremendously useful in applied mathematics. Most famously they were used by Dirac in his quantum mechanics; it is less well known that mathematical physicist Kirchhoff used them decades earlier in his work on optics. The theory of distributions is attractive and establishes a precise basis for the ideas which these notes will use.
As it turns out, Riesz also provided the essential tool for defining generalized functions:
Definition XV.6. We define some useful function spaces on an
arbitrary open set 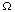 in Rn as follows:
in Rn as follows:
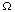 ] is the set of
bounded, continuous functions on
] is the set of
bounded, continuous functions on
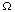 .
.
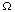 ] is the subset of
C[
] is the subset of
C[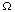 ]
consisting of functions which are equal to zero outside some closed,
bounded region in
]
consisting of functions which are equal to zero outside some closed,
bounded region in 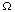 .
(You may recall that a closed, bounded set in Rn
is called compact.)
.
(You may recall that a closed, bounded set in Rn
is called compact.)
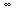 [
[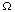 ] is the set of functions
f in Cc[
] is the set of functions
f in Cc[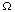 ]
such that all derivatives of f are also in
Cc[
]
such that all derivatives of f are also in
Cc[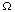 ].
These are also known as test functions.
].
These are also known as test functions.
The uniform sense of convergence is appropriate for these spaces: Any uniform limit of continuous functions on a fixed bounded set is a continuous function. When we say that a sequence of test functions converges, we mean that the set where the sequence differs from zero is contained in a fixed, bounded region, and not only does the sequence fk(x) converge uniformly, but so do all of its derivatives. It sounds like a lot to ask for a function to be a test function, and you may even be suspicious that there aren't too many of them. However, it is known that any L2 function can be approximated in the r.m.s. sence by test functions, though not in generally in the uniform sense.
Theorem XV.7. (The Riesz-Markov representation theorem.)
Suppose that T[f] is a continuous linear functional on the set of test functions
Cc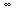 [
[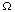 ]
and is positive in the sense that for any positive test function
f(x), T[f]
]
and is positive in the sense that for any positive test function
f(x), T[f]
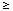 0. Then T[f] may be considered
as an integral, formally written as
0. Then T[f] may be considered
as an integral, formally written as
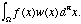
The same theorem is true with
Cc
in place of
Cc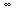 .
We shall
return to the delta function when its properties are needed to
understand how to construct
Green
functions.
.
We shall
return to the delta function when its properties are needed to
understand how to construct
Green
functions.
As suggested in the previous two chapters, the role of the adjoint of a linear function will be critical. If L is a linear function that is defined on some subspace of E, then the task of finding the adjoint L* will involve finding not only how the adjoint is defined, but also what is the subspace composing the domain of definition of L*.
In linear algebra, the adjoint of a square matrix is given by its transpose (if necessary also taking the conugate of any matrix entries which are complex numbers). How can the adjoint be defined for general linear operators?
Definition XV.8. Suppose that L is a continuous linear operator on a Hilbert space. Its adjoint L* is the unique linear operator such that for all f, g,
adjoint Definition XV.9. Suppose that L is a linear operator defined on a subspace M of a Hilbert space. The adjoint domain M* is the set of vectors f in the Hilbert space such that for all g in M, the linear functional
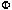 g[f] := <f,Lg>
g[f] := <f,Lg>
A differential operator is not really defined until we specify its domain of definition, and the issue of finding the domain can be technically quite involved. Usually there are two parts sorts of questions about the domain, one having to do with precisely how differentiable the functions must be (which leads into some advanced theory about regularity of functions), and the other having to do with boundary conditions. That is, how can you restrict the functions in M to make sure that when you integrate by parts in order get (15.3), there are no boundary contributions.
In what follows, we shall ignore the question of regularity and discuss only the boundary conditions when we spell out domains of definition of operators.
Consider the differential operator L given by
We can define the formal adjoint L* of L by
(15.4)
The formal adjoint is exactly what you get when you integrate by parts enough times to obtain the formula (15.3) if you ignore all boundary terms. The second order operator L(y) = a2(x) y''(x) + a1(x) y'(x) + a0(x) y(x), according to this formula, will have formal adjoint
L*(y) = (a2(x) y(x))'' - (a1(x) y(x))' + a0(x) y(x).
If L is not defined on all of E, but just some subspace, or manifold M, then one must find where L* is defined. We denote the domain of L* by M*.
As remarked abovee, The TRUE adjoint L* has to satisfy (15.3), which for a differential operator on the interval [0,1] reads:
(15.5)
for all u in M and v in M*. It is often useful to use the following identity resulting from integration by parts:
Model Problem XV.10. Let L = D2 + 3 x D + x2 1. That is, L(u) = u''(x) + 3x u'(x) + x2 u(x). Let us specify that the operator L is defined on the manifold consisting of all regular functions u on [0,1] which satisfy u(0) = u'(1) and u(1) = u'(0). Thus:
Solution. L* will have the form of the formal adjoint:
L*(v) = v'' - (3x v(x))' + x2v(x).
The manifold M* is chosen to make the equation
< L(u), v> = < u, L*(v) >
satisfied.
Since u is in M, u'(1) = u(0) and u(1) = u'(0), so that
< L(u), v > - < u, L*(v) > = [v(1) + v'(0)]u(0) - v'(1) + v(0) - 3v(1)] u'(0).
In order for this last line to be zero for all u in M, the manifold M* should consist of functions f such that
v(1) + v'(0) = 0 and v'(1) + v(0) = 3v(1).
QED
The boundary-value problem y''+ 3y' + 2y = f , y(0) = y'(0) = 0 leads to an operator L and a manifold M given by
For such problems, we will have techniques to construct G. In this case
Most frequently, we will consider three types of boundary conditions illustrated below for a second order problem:
Initial conditions
unmixed, two point boundary conditions
mixed, two point boundary conditions
Before developing a technique for solving these ordinary differential equations with boundary conditions, attention should be paid to the statement of the Fredholm Alternative Theorems in this setting. You may wish to compare it with the alternative theorems for integral equations and for matrices.
Theorem XV.12. Suppose that L is an nth order differentiable operator with n boundary conditions. B1, B2, ...Bn. The problem is posed as follows: Given f, find u such that L(u) = f with Bp(u) = 0, p = 1, 2, ...n.
I. Exactly one of the following two alternatives holds:
(a)(First Alternative) if f is continuous then L(u) = f, Bp(u) = 0, p = 1, 2, ..., n, has one and only one solution..
(b)(Second Alternative) L(u) = 0, Bp(u) = 0, p = 1, 2, ...n, has a nontrivial solution.
II. (a) If L(u) = f, Bp(u) = 0, p = 1, 2, ...n, has exactly one solution then so does L*(u) = f, Bp*(u) = 0, p = 1, 2, ...n have exactly one solution.
(b) L(u) = 0, Bp(u) = 0, p = 1, 2, ... n, has the same number of linearly independent solutions as L*(u) = 0, Bp*(u) = 0, p = 1, 2, ...n.
III. Suppose the second alternative holds. Then L(u) = f, Bp(u) = 0, p = 1,
2, ...n has a solution if and only if < f, w > = 0 for each w that is a
solution for
L*(w) = 0, Bp*(w) = 0, p = 1, 2, ...n.
 (x),
it will be true that
(x),
it will be true that
 > =
<f, L*
> =
<f, L* > =
<g,
> =
<g,  >
(15.6)
>
(15.6)
 , and f is also sufficiently regular
to allow integration by parts, then we know that L f = g. (Boundary
terms do not arise because the test functions zero them all out.)
, and f is also sufficiently regular
to allow integration by parts, then we know that L f = g. (Boundary
terms do not arise because the test functions zero them all out.)
This means that we can tell that L f = g without directly differentiating f. hence, even if f is not differentiable, we can say that in a certain sense, L f = g:
Definition XV.13. A generalized function f solves
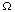 provided that (15.6) holds for all
test functions
provided that (15.6) holds for all
test functions  on
on
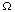 .
.
Notice that although we have been talking about ordinary differential equations, this definition is meaningful for partial differential equations, or, for that matter, equations which involve other operations besides differentiation.
Examples XV.14.
Actually, the previous three examples work for any
function h of a single variable in place of the Heaviside function H.
We leave the verification of these equations to the Exercises.
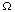 = R, dH(x)/dx =
= R, dH(x)/dx =
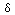 (x).
(x).
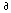 u/
u/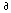 x -
x -
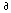 u/
u/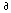 t = 0.
t = 0.
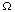 = R2,
H(x-t) is a weak solution of the wave equation
= R2,
H(x-t) is a weak solution of the wave equation
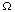 = R2,
H(x+t) is a weak solution of the wave equation
= R2,
H(x+t) is a weak solution of the wave equation
XV.1. Calculate the following integrals:
XV.2. Let <f,g> denote the standard inner product for 0 <= x <= 1.
Find a generalized function g(x) such that
XV.3. Compute the formal adjoint for each of the following:
(a) L(y) = x2 y'' + x y' + y (b) L(y) = y'' +
9  2 y
2 y
(c) L(y) = (ex y'(x))' + 7 y(x) (d) L(y) = y'' + 3y' + 2y
XV.4. Argue that L is formally self adjoint if it has constant coefficients and derivatives of even order only.
XV.5. Suppose that L(y) = y'' + 3y' + 2y and y(0)= y'(0) = 0.
Find conditions on v which assure that
XV.6. Let L(u) = u'' + u. The formal adjoint of L is given by L*(v) = v''+ v. For each manifold M given below, find M* such that L* on M* is the adjoint of L on M.
(a) M = {u: u(0)=u(1)=0},
(b) M = {u: u(0)=u'(0)=0}
(c) M = {u: u(0)+3u'(0)=0, u(1)-5u'(1)=0},
(d) M = {u: u(0)=u(1), u'(0)=u'(1) }.
(Answers)
XV.7. Let L and M be as given below; find L* and M*.
(a) L(u)(x) = u''(x) + b(x) u'(x) + c(x) u(x),
M = {u: u(0)=u'(1), u(1) = u'(0) }.
(b) L(u)(x) = -(p(x) u'(x))' + q(x) u(x);
M = {u: u(0) = u(1), u'(0) =u'(1) }.
(Hint) (c) L(u)(x) = u''(x);
M = {u: u(0) + u(1) = 0, u'(0) - u'(1) = 0 }
(Answers)
XV.8. Verify that for L, M, and u as given in Model Problem XV.11, u is in M and L(u) = f. (Recall Exercise 3 in the introduction to the problems of Green functions.)
Suppose G is as in Model Problem XV.11, and
Show that z solves L* z = h for z in M*.
XV.9. Decide whether the following operators L are formally self adjoint, and whether they are self adjoint on M. Decide whether the equation L(y) = f on M is in the first or second alternative.
(a) L(y) = y'', M = {y: y(0) = y'(0) = 0 }.
(Answer)
(b) L(y) = y'', M= {y: y(0) = y(1) = 0 }.
(Answer)
(c) L(y) = y'' + 4  2y, M={y: y(0) = y(1), y'(0) = y'(1)}.
2y, M={y: y(0) = y(1), y'(0) = y'(1)}.
(Answer)
(d) L(y) = y'' + 3y' + 2y, M = {y: y(0) = y(1) = 0}.
(Answer)
XV.10. Suppose that L(y)(x) = y''(x) + 4
 2y(x). B1(y) = y(0) and
B2(y) = y(1).
2y(x). B1(y) = y(0) and
B2(y) = y(1).
(a) Show that the problem L(y) = 0, B1(y)= B2(y) = 0 has sin(2  x) as a
non-trivial solution.
x) as a
non-trivial solution.
(b) What is the adjoint problem for {L, B1, B2}?
(c) What specific conditions must be satisfied by f in order that L(y) = f, y(0) = 0 = y(1) has a solution?
(d) Show that y''(x) + 4  2y(x) = 1, y(0) = 0 = y(1) has
2y(x) = 1, y(0) = 0 = y(1) has
[ 1 - cos(2  x) ] /4
x) ] /4  2 as a solution.
2 as a solution.
XV.11. Show that y'' = x, y'(0) = 0 = y'(1) has no solution.
XV.12. Show that y'' = sin(2  x), y'(0) = 0 = y'(1) has a solution.
x), y'(0) = 0 = y'(1) has a solution.
XV.13. Verify that the
differential equations in
Examples XV.14 have the weak solutions stated there.
Hint for the wave equation. Change variables to r = x+t and s = x-t.