XIV. Solving Y = KY + f.

Linear Methods of Applied Mathematics

Evans M. Harrell II and James V. Herod*

*(c) Copyright 1994,1997,2000 by Evans M. Harrell II and James V. Herod. All rights reserved.

version of 11 May 2000

Here is a Mathematica notebook with calculations for this chapter, and here are some Maple worksheets with similar calculations:

  • Separable kernels
  • Small K(x,t)
  • Small K*(x,t)
  • Neither small nor separable

    • XIV. Solving Y = KY + f (continued)

    In case K neither has a separable kernel nor is small, then the next resort is to approximate K with an operator which has a separable kernel.

    Theorem. If

    then there are kernels Kn and G such that

    (1) K = Kn + G,

    (2) Kn has a separable kernel,

    and

    In the succeeding pages, we show how to compute Kn and G. However, we first illustrate that the problem is - in theory - solved if we have such a resolution of K into Kn and G. We seek y such that

          y = Ky + f = Kny + Gy + f

    or       y - Gy = Kny + f.

    Use the resolvent for G:

           (1-G)-1 = 1 + RG,

    to get that

    y = Kny + RG(Kny + f) + f

    =[Kn + RGKn]y + (RGf + f).

    Define z to be RGf + f, or, what is the same, solve the equation

    z = Gz + f.

    We can solve this equation because G is small. Now, we seek y such that

    y = (Kn + RGKn)y + z.

    Re-writing this as an integral equation, we seek y such that

    where

    What is astonishing is that this last integral equation is separable! To see this, suppose

    Then

    So, here is the conclusion. If K is Kn + G as in the above Theorem, in order to solve y = Ky + f, use the fact that

    to form the resolvent for RG; then find z such that z = (1+R G)f. Finally, solve the separable equation y = (Kn + RGKn)y + z 

                                                                              QED

    We now must address the question of how to achieve the decomposition of K into Kn + G. The ideas are familiar to us from chapter IV on Fourier series. In summary of those ideas, recall that if p and q are integers, then

    We seek Apq such that

    In fact, by integrating both sides of this last equation after multiplying by sin(m pi x) sin(n pi y), we have

    From the theory of Fourier series,

    in the sense that

    as n -> * . Let n be an integer such that

    Define Kn and G by

    and       G = K - Kn.

    Then these three requirements are met:

    (1) K = Kn + G,

    (2) Kn is separable,

    and

    Thus, we have an analysis of an integral equation y = Ky + f where

    The engineer will want to know about approximations. Here are two appropriate questions:

    (a) Suppose one hopes to solve y = Ky + f and that Kn is separable and approximates K. How well does the solution u for u = Kn u + f approximate y?

    (b) Suppose K = Kn + G and


    Gp approximates RG. How well does the solution u for

           u = [Kn+ SKn] u + [1+S ]f

    approximate y?

    Exercises XIV
    1. With K, f, and an interval as given, solve the integral equation y = Ky + f.

      (a) K(x,t) = 2x-t, f(x) = x2 on [1,2].

      ans: y(x) = x2 - (75x - 61)/6. (b) K(x,t) = x + 2xt, f(x) = x on [0,1]. ans: y(x) = -6x. (c) K(x,t) = 2x2 -3t, f(x) = x on [0,1]. ans: y(x) = x +(6x2-13)/28.

       (d) K(x,t) = t(t+x), f(x) = x on [0,1] ans: y(x) =(18+48x)/23. (e) K(x,t) = xt2+1, f(x) = x on [0,1] ans: y(x) = -3. (f) K(x,t) = 1/2 + x t, f(x) = 3x2-1 on [-1,1]. ans: y(x) =3x2 + c (g) K(x,t) = x t, f(x) = exp(x) on [0, ln(7)]. ans: y(x) = ex+ax where a = 3(7ln(7)-6)/(3-(ln(7)3 (h) K(x,t) = x - t, f(x) = x on [0,1]. ans: y(x) = (18x-4)/13 (i) K(x,t ) = sin(pi x) cos(pi t), f(x) = sinh(x) on [0,1].
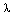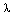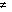    2. Show that if f is continuous and 1 + lambda /2 - lambda 2/240 != 0,

      then

      y(x) = -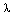lambda I(0,1, ) ( x2 t + x t2 ) y(t) dt + f(x)

      has a solution.

    3. (a) For what functions f does the equation have a solution?

      (Answer)

    4. Solve the integral equation y = Ky + f where

      and f(x) = x. (Hint: take the derivative of both sides.)

      (Answer)

    5. Let

      (a) Show that if 0 <= x <= 1,

      In fact,

      (b) Toward solving y(x) = K[y](x) + x , compute phi 0, phi 1, and phi 2.

      (Answer)

      (c) Give a bound on the error between the solution y and phi 2.

                  

      ans: |y - phi 2| <= 1/4 (d) Solve y(x) = Ky(x) + x in closed form for this K. (Reference: Exercise 4.)
    6. Repeat (a)-(c) of the previous exercise with

      (Answer)

    7. Find the solution of the following integral equation, or else explain why there is no solution: u(x) = 1 + int((x sin(pi y) + y sin(pi x)) u(y), y=0..1.
    8. Suppose that

      Give a formula for

    9. Compute

      for each K in the previous exercise set.                

      ans: 1/12 and 1/6.
    10. Let

      For this K, find y such that y(x) = Ky(x) + x. Note that

      What is the significance of this observation?

                     

      ans: x +1/8
    11. Let

      For this K, find y such that y(x) = Ky(x) + x. Note that

      What is the significance of this observation?

                     

      ans: exp(x) - 1
    12. 5. Suppose that

      so that the kernel of K is cos(x+t) and the kernel of H is sin(x+t). What is the kernel of K[H]?

      (Answer)

    13. Find the kernel for the resolvent of the K whose kernel is K(x,t) = x t.

                  Ans: R(x,t) = K(x,t) + K2(x,t) + K3(x,t) + . = 3xt/2.

    14. Consider the problem

      (a) Explain how you know this problem is in the second alternative.

      ans: y(x) = c is a non-trivial solution to the homogeneous problem. (b) Find linearly independent solutions for the equation y=K*(y).

      (c) Let f1(x) = 3x - 1 and f2(x) = 3x2 - 1. For one of these there is a solution to the equation y = K(y) + f, for the other there is not. Which has a solution?

          (Answer)

      (d) For the f for which there is a solution, find two.

          (Answer)

    15. Consider the problem

      (a) Show that the associated K is small in both senses of this section.

      (b) Compute phi2 where f(x) = 1.

          (Answer)

      (c) Give an estimate for how much phi2 differs from the solution y of y=K(y)+f.

          (Answer)

      (d) Using the kernel K for K, compute the kernel K2 for K2 and K3 for K3.

          (Answer)

      (e) Compute the kernel for the resolvent of this problem.

          (Answer)

      (f) What is the solution for y=Ky+f in case f(x) = 1.

          (Answer)

    16. Consider the problem

      (a) Compute the associated approximations \phi0, \phi1, \phi2, and \phi3.

          (Answer)

      (b) Give an estimate for how much \phi3 differs from the solution.

      (c) Give the kernel for the resolvent of this problem.

          (Answer)

      (d) Using the resolvent, give the solution to this problem.

          (Answer)

      (e) Using the fact that the kernel of the problem separates, solve the equation.

    17. Suppose that

      (a) Show that

      (b) Solve the problem y = K[y] + 1.

          (Answer)

    18. (a) Find a nontrivial solution for y = K[y] in L2[0,1] where

            K(x,t) = 1 + cos(pi x) cos(pi t).

      (b) Find a nontrivial solution for z = K*[z].

      (c) What condition must hold on f in order that

            y = K[y] + f

      shall have a solution? Does f(x) = 3 x2 meet this condition?

          (Answer)

    19. Suppose that

      so that the kernel of K is cos(x+t) and the kernel of H is sin(x+t). What is the kernel of K[H]?

      Answer

    20. Verify the solution found in Model Problem XIV.5
    Link to
  • chapter XIV (first part)
  • chapter XV
  • Table of Contents
  • Evans Harrell's home page
  • Jim Herod's home page