Linear Methods of Applied Mathematics
Evans M. Harrell II and James V. Herod
version of 30 August 2000.
We begin by discussing the potential equations of Laplace and Poisson, which are discussed in Chapters VI, IX, and XIX. Our main tool will be integration by parts, as encapsulated by Green's identities.
The question we ask is the relationship between a function u(x) and its average value over a small sphere centered at x. The average would be expected to depend on the radius of the ball, which we'll call r. Thus:
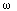 n
is the area of a sphere in n dimensions, of radius 1. Differentiating
with the vector chain rule, we get
n
is the area of a sphere in n dimensions, of radius 1. Differentiating
with the vector chain rule, we get
This formula has several interesting consequences:
Definition PR.1. A function is harmonic if it satisfies Laplace's equation,
 2u
2u
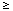 0.
0.
 2u
2u
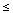 0.
0.
From (pr1) we get the following theorem:
Remarks about the proof.
Replacing the spheres by the balls in parts 1 and 2
is merely a matter
of performing an additional integration over r.
Other than that these statements are immediate from
(pr1). The converse, part 3,
also follows from that formula, with
contrapositive logic:
We consider the converse of part 1, as representative. Suppose that
 2u is continuous and not
equal to 0 at some point x. Then either there is some ball
centered at x where the right side of
(pr1) is positive, or else a ball
centered at x where the right side of
(pr1) is negative.
Whichever statement applies, U(r,x) changes as r varies,
which contradicts the mean-value property.
2u is continuous and not
equal to 0 at some point x. Then either there is some ball
centered at x where the right side of
(pr1) is positive, or else a ball
centered at x where the right side of
(pr1) is negative.
Whichever statement applies, U(r,x) changes as r varies,
which contradicts the mean-value property.
As an example of the physical consequences of this, consider heat flow, as in Chapter VIII. If the temperature distribution of a homogeneous body does not have the mean-value property guaranteed by Theorem PR.2 for harmonic functions, then it is not in equilibrium, and the temperature will redistribute itself.
The mean-value property is also related to the maximum principle, which was stated and proved for the heat equation in Chapter VIII. In the case of harmonic functions it reads as follows.
Theorem PR.3. Suppose that u is harmonic on an open region D. If u attains its maximum or minimum value within D then u must be a constant throughout D.
Another stetment of the maximum principle is that: for any closed region on which u is harmonic, its maximum and its minimum are attained on the boundary.
Finally, the maximum principle is an important tool for knowing when a problem is well-posed, for it implies a uniqueness theorem for Poisson's equation (see Chapter 19):
Theorem PR.4. Suppose that
 2u = f on D,
2u = f on D,
Proof. Let w(x) := u1(x) - u2(x). Then we know that w solves Laplace's equation and is identically 0 on the boundary of D. As a consequence of the maximum principle, both the maximum and the minimum of w in D must equal 0, which means that u1 = u2.
QED